이번 포스팅에서는 지난 학기 수강했던(Udacity) cs7838 (Artificial Intelligence for Robotics) 과목과 Jonathan Hui의 글을 번역하여 구성하였습니다. 모든 자료 위 강의와 포스팅에서 발췌했습니다.
대학교 시절, mpu6050 센서를 통해 각도를 계산하는 일이 필요했는데, 사람들이 칼만필터를 사용한다는 글을 본 적이 있습니다. 그 때는 칼만필터에 대한 이해가 전혀 없었던 시절이라 단순히 칼만 필터가 노이즈를 잡아준다고 생각했었는데요. 이번에 아주 깊게는 아니지만, 칼만 필터의 기초에 대해 공부하게 되면서 여러가지를 배우게 되어 내용을 기록하고자 합니다.
자율 주행의 주요 요소로는 Localization, Perception, Planning 등이 있습니다. 독립된 영역은 아니고 모두 종합적으로 고려되어 자율 주행을 만들어내게 되는데요. 칼만 필터는 localization과 perception의 연결고리 어딘가 즈음 있다고 생각이 됩니다. perception에 의해 인지하고, localization 즉 자동차나 특정 물체의 위치를 탐색하는 데 사용된다고 볼 수 있겠습니다.
칼만 핕터란?
칼만 필터는 현재 자동차의 위치에 대한 belief와, 센서 등을 통해 perception 즉 인지된 주변 정보를 종합하여 localization을 정확하게 예측하게 해주는 방법입니다. 즉, 현재 자동차가 어디에 있는지를 보다 정확하게 예측해주는 수학적 방법론입니다.
Stochastic model VS Deterministic model
이제부터 모든 내용은 stochastic model을 가정합니다. 모든 측정이나 예측은 정확한 것이 아니고, gaussian distribution 즉 정규 분포를 따라 형성된다는 얘기입니다. 칼만필터는 가우시안 분포가 아닐 경우에도 사용할 수 있는 일종의 개선된 방식도 존재하는데, 이번 포스팅에서는 모든 노이즈는 정규 분포를 따른다고 가정하고 시작하겠습니다.
Kalman Filter Intuition
칼만필터의 직관적인 이해를 위해 정지선 앞에 있는 자동차의 위치 추적 사례를 들어보겠습니다.
우리는 belief가 있습니다. 2m 앞에 정지선이 있다는 사실을요. 다만 이것은 믿음일 뿐이고, gaussian 분포를 따르고 있기 때문에 아래와 같이 현재 위치에 대한 확률 분포를 표시해볼 수 있습니다.
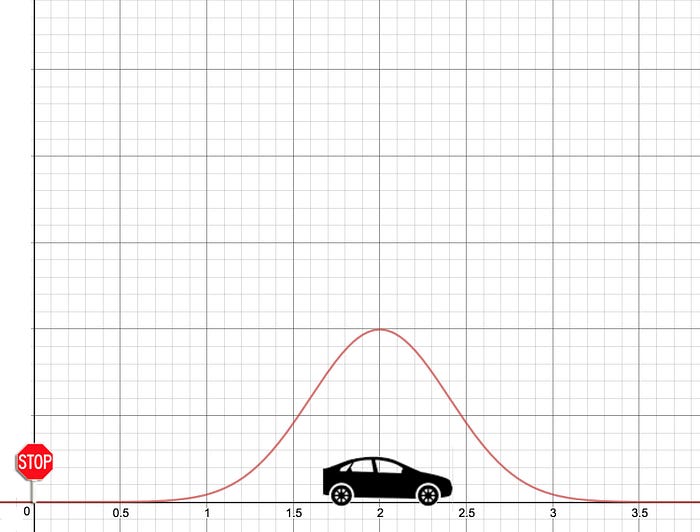
이번에는 단순히 belief가 아니라, measurement를 수행해봅니다. GPS를 통해 현재 차의 위치를 읽어보니 다음과 같이 3m 떨어져있다는 결과가 나왔습니다.
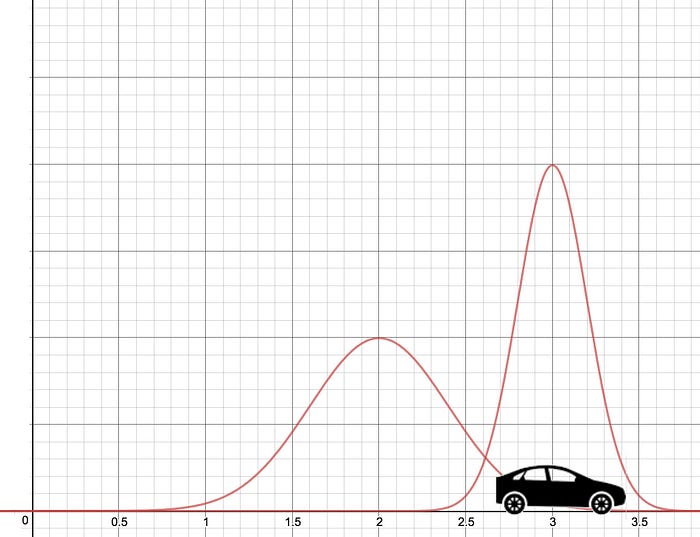
그렇다면 belief가 맞을까요, measurement가 맞을까요? 칼만 필터는 쉽게 얘기하면, 이 두 가지 그래프를 짬뽕해서 최적의 결과를 내놓는 방식입니다. 바로 아래 그림처럼요.
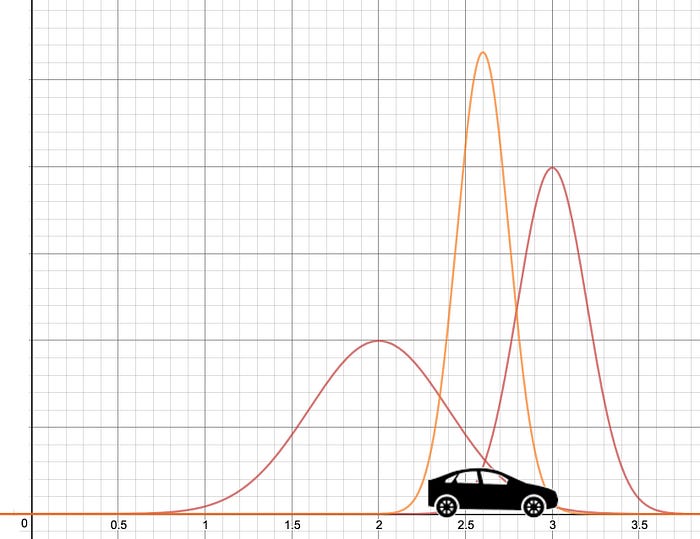
정규 분포는 평균과 표준편차로 보통 표기하는데, 위 그림을 보시면 평균은 두 평균의 중간 어디쯤으로 보이고, 표준편차를 훨씬 작아진 것을 볼 수 있습니다. 수식에 의하면 칼만 필터를 통해 나온 정규 분포는 새로운 평균과 새로운 표준편차를 갖는데, 각각의 값은 기존의 두 분포의 평균과 표준편차를 통해 연산이 됩니다. 두 그래프를 통해 예측된 결과물이기 때문에 표준편차가 적다, 즉 보다 정확하다 라고 직관적으로 이해해볼 수 있을 것 같습니다.
아래 그림처럼 두 정규 분포가 있다면, 공통된 지역을 통해 예측의 정확성을 올리는 과정이다라고도 볼 수 있겠네요.
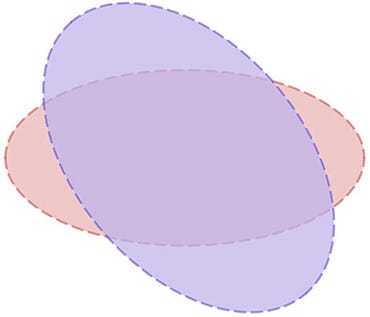
Kalman Filter의 belief는 prior, 예측 결과인 prediction는 posterior라고 표현합니다. 위 과정을 정리하면, 다음 2가지를 계속 반복한다고 보시면 됩니다.
Predict: 보통 자동차의 dynamic model를 활용하여 현재 위치를 예측하며, belief와 같습니다. 여기서 다이나믹 모델이란 흔히 얘기하는 물리 방정식들입니다.Update: 새로운 Measurement를 통해 predict와 짬뽕시켜서 위치를 갱신합니다. 이 과정을 계속 반복하면서 위치를 찾아내는 것이 칼만필터입니다.
칼만필터 수식들
복잡한 수식들에 대한 설명은 생략하겠습니다. 매트릭스의 연산으로 구성이 되는데, 대체로 라이브러리화 되어 있으며 정리하면 식은 다음과 같습니다.

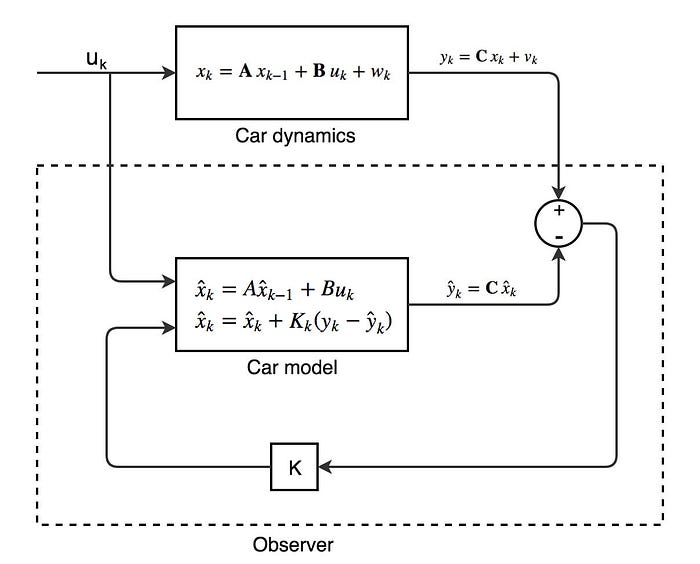
여기에 나오는 state-transition model이나, input control model 등은 생략했지만 주의깊게 볼 매트릭스가 2개 있습니다.
Q: Covariance matrix of process noise: 프로세스를 진행하는데 있어서 발생하는 노이즈. 아마도 prediction에 대한 노이즈 같습니다.R: Covariance matrix of measurement noise: 측정 노이즈. measurement할 때 발생하는 노이즈를 얘기합니다. (prediction 과정에서 연산)
노이즈가 0이라면 정규 분포의 평균은 고정이 될겁니다. 0이 아니라면 정규 분포의 평균점 자체에 노이즈가 발생할 수 있는 것 같고요. 노이즈에 따라 예측을 잘하기도하고 못하기도 합니다. 무조건 노이즈가 없는게 좋은 건 아닙니다. 예를 들어 센서 성능이 미흡해서, Measurement의 정확도가 너무 떨어지면 어떻게할까요? 정확도가 떨어지는데 노이즈를 0으로 셋팅하면, 수식 상 센서에서 측정된 수치를 믿는다는 의미가 됩니다. 따라서 성능이 잘 나올 수 없는 상황이 발생하곤 합니다. 반대로 노이즈가 0이 아니라면, 센서 성능이 간혹 떨어지는 상황이 오더라도, 인위적인 노이즈 덕분에 측정을 오히려 잘할 수 있는? 역설적인 상황들이 발생합니다. 노이즈는 필터를 사용하는 환경에 맞춰서 튜닝해야하는 파라미터로 알고 있습니다.
칼만필터 내용 정리
한번 더 자동차의 상황에 맞게 칼만필터를 정리해보겠습니다.
먼저 자동차의 과거 상태가 다음 그림과 같다고 합니다.
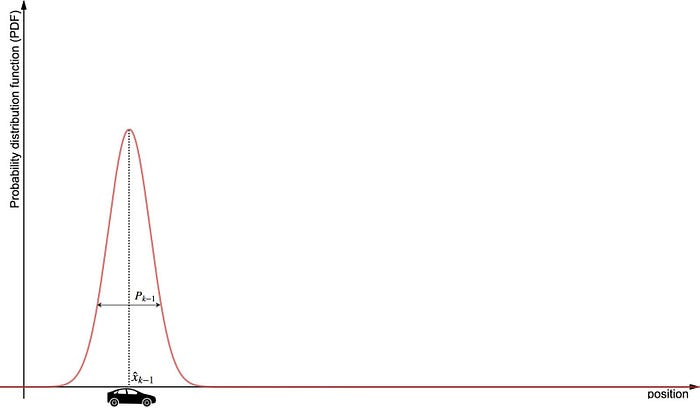
여기에 시간이 지나고, 물리 방정식에 의해 자동차는 다음과 같이 이동했습니다.
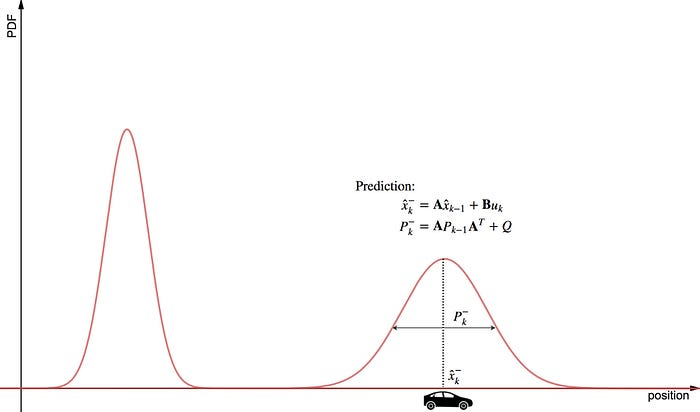
아직까지 측정한 것은 반영되지 않았습니다. 그저 belief에 의해 나온 prediction을 표현했을 뿐입니다. 이제 센서로부터 측정된 결과를 불러옵니다.
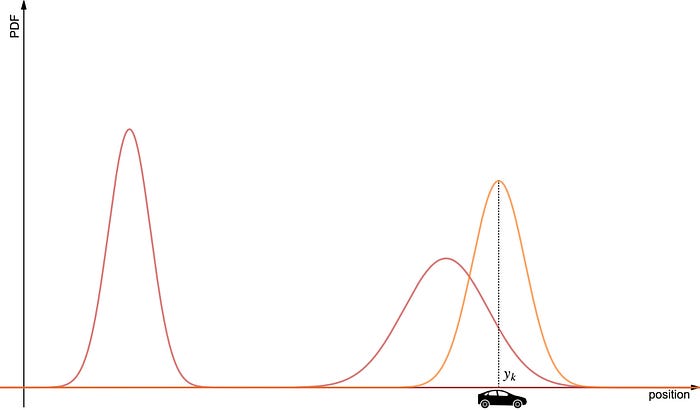
측정치로부터 계산된 위치는 우리의 belief보다 다소 앞서있네요. 이제 이 측정치와, 방금 전 계산했던 belief를 짬뽕시켜 Update하는 과정을 거칩니다. 그 결과는 아래와 같습니다.
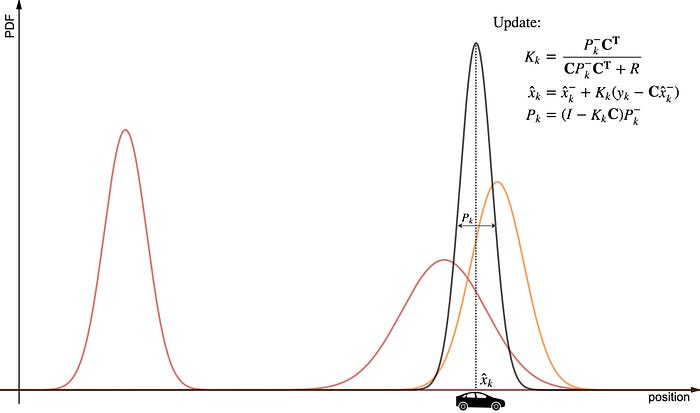
이제 다시 belief에 의해 prediction을 거치고, 또 update를 하면서 자율주행차는 현재 나의 위치, 즉 localization을 수행하게 됩니다.
다음 포스팅에서는 particle filter에 대해 알아보겠습니다.
'Developer > Artificial Intelligence' 카테고리의 다른 글
| Self driving car - Particle Filter 파티클 필터 (11) | 2021.12.29 |
|---|

댓글