이 글은 이 글을 번역+재구성한 글입니다. 모든 이미지나 내용 출처는 위 페이지임을 미리 밝힙니다.
지난 포스팅에서 간단히 Wavelet이 어떤 건지에 대해 설명했습니다. 이번 포스팅에서는 Continuous Wavelet Transform(CWT)와, Discrete Wavelet Transform(DWT)에 대해 알아보겠습니다.
CWT와 DWT, 뭐가 다른가요?
영어에서도 보듯, Continuous는 연속적이라는 뜻이고, Discrete은 이산적이라는 뜻입니다. 앞선 포스팅에서 scale와 shifting에 의해 wavelet이 동작한다고 말씀드렸는데요.
CWT는 scale과 shifting이 continuous, 즉 연속변수로 작동합니다. 따라서 아래 수식으로 나타낼 수 있습니다. a는 scale factor, b는 shift factor입니다. 연속적이기 때문에 무한한 wavelet들을 scaling하고 shifting할 수 있습니다.
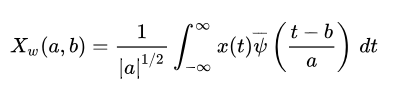
이에 비해 DWS는 a, b가 이산적인 값입니다. a는 2의 배수로 움직이며, b는 증가하는 정수 값으로 표현합니다.
일반적으로 CWT는 스펙트로그램을 얻는데 사용하고, DWT는 신호의 노이즈 처리에 사용합니다.
DWT에 대해서
DWT는 filter-bank로서 적용된다고 할 수 있습니다. 즉, DWT는 흔히 말하는 high pass filter, low pass filter 로서 작용합니다.
DWT를 적용할 때는 smallest scale, 즉 가장 작은 스케일부터 시작합니다. 즉 고주파를 탐색할 수 있게 됩니다. 그러면서 스케일을 늘려가면서 저주파까지 탐색하게 되는 구조입니다.

파이썬의 wavelet 라이브러리를 활용하면, 위의 approximation과 detail coefficient 값을 구할 수 있습니다. 즉, high pass와 low pass filter로 활용할 수 있습니다.
PyWavelets의DWT라이브러리를 활용합니다. (pywt.dwt())- DWT는 두개를 return합니다. Approximation과 Detail Coefficient입니다.
Approximation: low pass filterDetail: high pass filter- DWT로 나오는 approximation의 결과값을 다시 DWT하면, 또 approximation과 detail을 각각 얻습니다.
- 이런 방식을 통해 신호 노이즈 처리에도 사용할 수 있습니다.
CWT는 머신러닝에 활용
앞서 CWT는 스펙트로그램을 생성할 수 있다고 말씀드렸습니다. 즉, 어떤 시그널에 대한 시간 정보와 주파수 정보를 모두 갖고 있고, 이를 이미지처럼 2차원 vector array로 표현할 수 있습니다. 이를 이용하면 퓨리에 변환이나 MFCC 등의 방법과 유사하게 머신러닝에 활용할 수 있습니다. 상세는 원본 글을 참조하실 수 있으며, 대략적인 이미지는 아래와 같습니다.

위와 같이 소리마다 특징을 이미지화할 수 있기 때문에, 머신러닝으로 활용이 가능합니다.대표적으로 CNN을 이용해 컨볼루션을 돌릴 수 있습니다.

이처럼 CWT는 보통 스펙트로그램을 생성하는 데 의미가 있으며, 결과물은 머신러닝으로 활용이 가능합니다. DWT는 위에서 설명드렸듯이 주파수 필터로서 역할할 수 있습니다.
DWT를 이용한 Deconstructing
시그널을 말그대로 deconstructing하는 데는 DWT를 활용합니다. 신호의 노이즈처리가 대표적인 예가 되겠습니다.
pywt.dwt(): 시그널의 approximation coefficient를 구할 수 있습니다. 그 coefficient에 또 dwt를 적용하면 할수록 low pass filter로서 활용할 수 있습니다.pywt.wavedex(): 위 과정을 함수화해놓은 메소드입니다.
아래 코드를 활용하면 고주파를 날림으로써 low pass filter를 구현할 수 있습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | DATA_FOLDER = './FEMTO_bearing/Training_set/Bearing1_1/' filename = 'acc_01210.csv' df = pd.read_csv(DATA_FOLDER + filename, header=None) signal = df[4].values def lowpassfilter(signal, thresh = 0.63, wavelet="db4"): thresh = thresh*np.nanmax(signal) coeff = pywt.wavedec(signal, wavelet, mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode="soft" ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = plt.subplots(figsize=(12,8)) ax.plot(signal, color="b", alpha=0.5, label='original signal') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'k', label='DWT smoothing}', linewidth=2) ax.legend() ax.set_title('Removing High Frequency Noise with DWT', fontsize=18) ax.set_ylabel('Signal Amplitude', fontsize=16) ax.set_xlabel('Sample No', fontsize=16) plt.show() | cs |
이 때 파라미터로 wavelet function이나 thresh의 값, mode 등이 있는데 이에 대한 상세 포스팅은 다음에 다시 올리겠습니다.
위 함수를 사용하면 아래와 같이 노이즈르 필터링할 수 있습니다.

보시는 바와 같이 노이즈가 큰 신호의 큰 흐름들만 잡아낼 수 있습니다. wavelet의 종류에 따라 노이즈를 더 잡아낼수도 있고, 덜 잡아낼수도 있어서 상황에 맞는 적절한 파라미터 선정이 필요합니다.
다음 포스팅에서는 Wavelet function의 종류에 따른 노이즈 처리 정도에 대해 포스팅해보겠습니다.
'Developer > Python' 카테고리의 다른 글
| [셀레니움 테스트] 테스트 (2) | 2021.06.07 |
|---|---|
| Wavelet Transform 기본개념 및 Fourier Transform 비교 (1) | 2020.10.23 |
| [파이썬 셀레니움] 프라이탁 신제품을 실시간으로 확인하기2 (13) | 2020.09.04 |
| [파이썬 셀레니움] 프라이탁 신제품을 실시간으로 확인하기1 (109) | 2020.09.03 |
| [Python] 구글번역 API를 통해 파워포인트, 엑셀 번역하기 (0) | 2020.09.03 |


댓글