본 글은 이 글을 번역 + 재구성한 글입니다. Fourier Transform 기반의 MFCC 등을 이용한 음성 데이터 분석 방법들에 대한 포스팅은 찾기 쉬운데, Wavelet Transformation에 대해서는 한글로 된 글이 많이 없어서 포스팅하게 되었습니다. 여러 글로 나눠서 올리도록 하겠습니다.
시작하기 전에..
이전에 제가 올린 퓨레에 변환과 MFCC에 대한 포스팅을 먼저 보고오시면 이해가 더 빠를 것 같습니다.
Introduction
위에서 제가 언급한 글들을 요약하자면 다음과 같습니다: 음성 데이터의 원형인 signal을 time-domain에서 frequency-domain으로 변환시켜주는 것이 바로 퓨리에 변환입니다. 또한 STFT(Short time Fourier Transformation)을 사용한다면, 작은 시간 단위마다 주파수 도메인으로 변환함으로써 스펙트로그램 형태의 컨투어 이미지를 얻는 것이 가능합니다. 이를 활용해 CNN과 같은 딥러닝에도 활용할 수 있습니다.
이번 포스팅에서는 Fourier Transform의 한계와, Wavelet의 장점 및 사용 방법에 대해 설명해보겠습니다.
Fourier Transform부터 Wavelet까지
아래 이미지는 일반적으로 얘기하는 퓨리에 변환입니다. 각각의 Signal이 있을 때, 이에 대한 퓨리에 변환을 시행하면 주파수 도메인의 그래프를 얻을 수 있습니다.
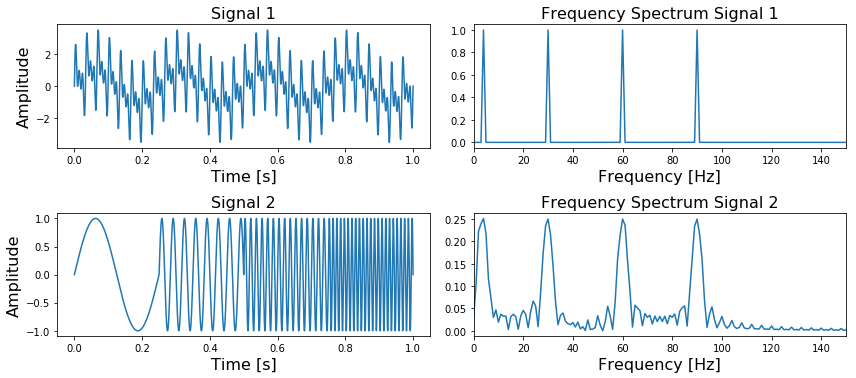
다만 그림에서 보다시피, 실제 시그널은 시간에 따라 변동이 발생하는데, 퓨리에 변환의 결과물인 주파수 그래프는 시간에 대한 정보를 담고 있지 않습니다. 즉, 특정 시간마다 변하는 주파수를 표현할 수 없습니다. 이를 해결하기 위한 방법으로 Short Time Fourier Transform이 있는데, 이는 RAW Signal을 국소 시간 단위로 쪼갠 뒤, 각각의 쪼개진 window 마다 퓨리에 변환을 하는 것입니다. 그리고 각 시간 window마다 나온 주파수 도메인의 그래프를 쭉~ 이어 붙이면 스펙트로그램을 얻을 수 있게 됩니다. 이렇게 만들어진 스펙트로그램은 주파수 도메인 그래프들이 특정 시간 주기로 연결된 것이기 때문에, 시간에 대한 정보도, 주파수에 대한 정보도 담고 있습니다. (상세 내용은 처음에 언급드린 5개의 글에서 확인하실 수 있습니다.)
그러나 STFT의 경우 한계가 있습니다. 바로 불확정성 원리(Uncertainty Principle)입니다. 위에서 STFT가 특정 시간 단위로 신호를 쪼갠다고 말씀드렸는데, 이 시간 단위와 주파수 해상도 단위가 Trade-off 관계에 있게 됩니다. (상세 식은 위키에서 볼 수 있습니다.) 즉, 주파수 해상도를 높이고 싶으면, 주파수를 분해하는 시그널 자체의 길이가 길어야되는데, 그렇게 되면 시간 단위는 길어지게 됩니다.
이를 해결하기 위한.. 이라기보다는 이런 한계를 극복한 방법이 바로 Wavelet Transform입니다. 퓨리에 변환이 수 많은 sin함수들로 시그널을 쪼개는 것이었다면, wavelet은 방법이 조금 다릅니다. 특정 신호의 scale과 shifting을 통해 시간 간격 및 주파수 해상도를 그때그때 다르게 가져갈 수 있다고 하는데요. 아래 도표를 보시면 이해가 쉽습니다.
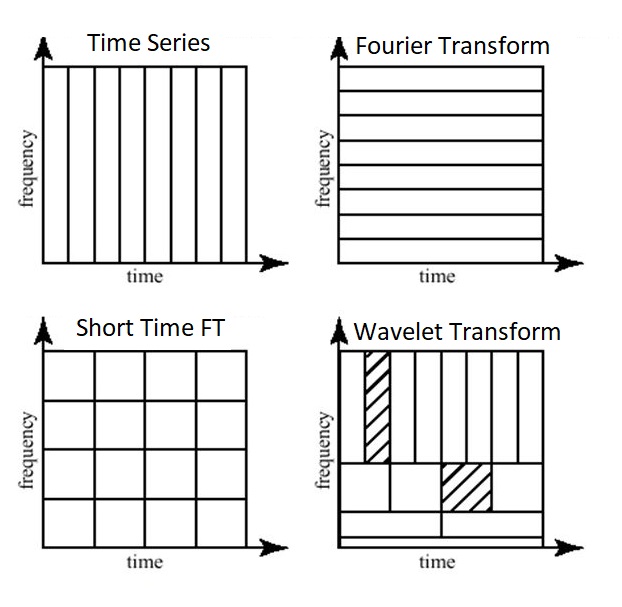
보시는 것처럼, Wavelet Transform의 경우 불규칙적으로 시간과 주파수 단위가 쪼개지는 것을 알 수 있습니다. 높은 주파수 해상도가 필요한 경우, 시간 단위를 길게 가져가면 되고, 높은 시간 해상도가 필요할 경우 주파수 해상도를 낮출 수 있는 것입니다.
How does the Wavelet Transform work?
퓨리에 변환이 sin함수를 사용하는 것과 다르게, wavelet은 wavelet이라는 함수를 사용합니다. 함수에 대한 내용은 여기에서 확인하실 수 있는데요.
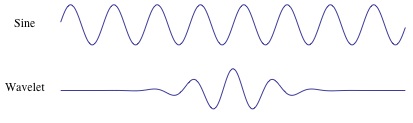
퓨리에 변환은 infinite한 sine wave에 기반한 반면, wavelet은 보시는 것처럼 그렇지 않습니다. 영문으로는 localized in time 이라고 적혀있는데요. 이러한 특징 덕분에 wavelet transform도 시간에 대한 정보를 담아낼 수 있다고 합니다.
즉, 시간에 대한 정보를 담아낼 수 있기 때문에, 특정 시간에 따라 wavelet function의 scale을 다르게 적용할 수 있습니다.
wavelet function을, convolution 방식을 이용하여 처음부터 끝까지 signal 전체에 연산을 하게 됩니다. 다 하게 되면, scale을 변경해가면서 다시 convolution을 돌리는 방식입니다. 이렇게 scale에 따른 스펙트로그램을 생성할 수 있습니다.
여기서 만들어진 스펙트로그램은 STFT를 통해 얻은 스펙트로그램과 차이가 있습니다. STFT는 단순 퓨리에 변환의 연속이기 때문에 frequency 스케일로 연산이 되지만, wavelet의 경우 위 wavelet function의 scale로 단위가 나타나게 되기 때문에, 실제 주파수를 보기 위해서는 아래와 같은 수식 연산이 필요합니다.
Fa는 pseudo-frequency이며, Fc는 wavelet의 central Frequency, a는 scaling factor입니다. 수식에서 보듯, scale factor인 a가 클수록 pseudo-frequency는 작아지는 것을 볼 수 있습니다. 즉, wavelet의 스케일이 클수록 주파수 해상도를 높게 얻어낼 수 있습니다.
여기까지가 대충 번역한 내용이지만, 사실 수식적으로 쉽게 납득이 가진 않습니다. 일단 넘어가도록 하겠습니다.
Wavelet Functions
다양한 wavelet function들이 있습니다. Wavelet 함수는 2가지 수학적 조건만 만족하면 되기 때문에, 새로운 형태의 wavelet 함수를 만드는 것이 용이합니다.
- finite energy
- zero mean
어쨌든 상세한건 잘 모르겠지만, 이런 형태로 만들어진 wavelet 함수들을이 여기에서 확인할 수 있습니다. 아래 그림은 그 예제들입니다.
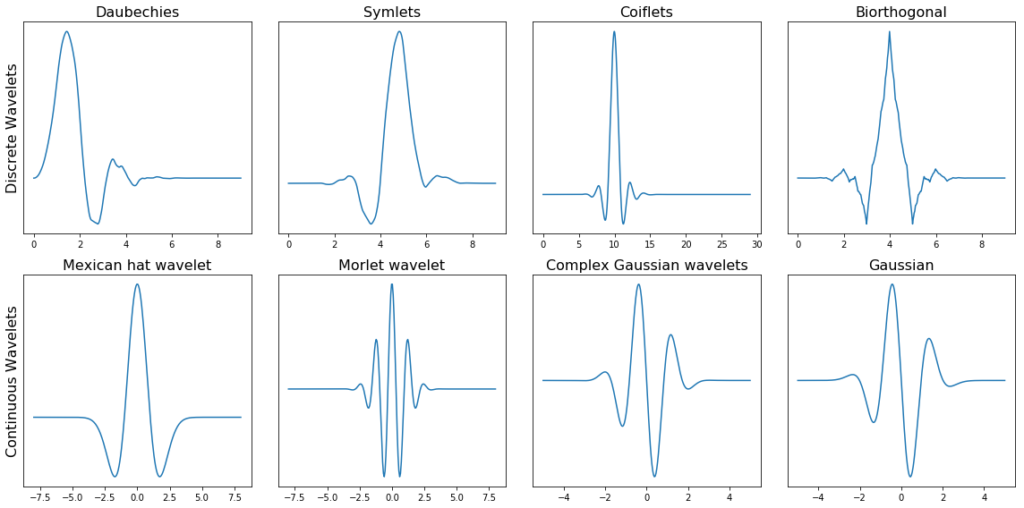
지금까지 Wavelet Transform이 어떤 건지 간단히 알아봤습니다. 여기 좋은 유튜브 영상이 있으니, 같이 보시면 도움이 될 것 같습니다. 다음 포스팅에서는 Continuous / Discrete Wavelet Transform에 대해 각각 알아보고 파이썬을 이용해 활용하는 법에 대해 포스팅해보겠습니다.
'Developer > Python' 카테고리의 다른 글
| [셀레니움 테스트] 테스트 (2) | 2021.06.07 |
|---|---|
| Continuous, Discrete Wavelet Transform (CWT, DWT) (1) | 2020.10.24 |
| [파이썬 셀레니움] 프라이탁 신제품을 실시간으로 확인하기2 (13) | 2020.09.04 |
| [파이썬 셀레니움] 프라이탁 신제품을 실시간으로 확인하기1 (109) | 2020.09.03 |
| [Python] 구글번역 API를 통해 파워포인트, 엑셀 번역하기 (0) | 2020.09.03 |


댓글