지난 포스팅을 요약하자면,
1. 드론 자세제어에는 PID가 필요하다.
2. PID란, 비례 적분 미분의 약어이다.
3. PID의 원리를 진자운동에 비유했는데, 이를테면 드론을 10도 기울여라~~ 란 명령을 주면, 드론은 사실은 11도까지 기울었다가, 다시 출력 조절하여 9도를 왔다가~ 다시 출력조절되서 10.5도갔따가~ 이러다가 10도에 딱 오게 된다는 것.
쉽게 얘기해서 위와 같은거고, 이제는 조목조목 따져보자.
PID 이해를 위해 가장 중요한 것은, 바로 오차의 개념이다. 오차란? 말 그대로 오차다. 위에서 예를 들었듯이 만약 드론이 지금 수평상태로 있는데 내가 10도 기울이란 명령을 줬다고 하자. 그렇다면 지금 오차는 바로 10도가 되는 것이다. 시간이 흘러 드론이 11도까지 왔다면 오차는 -1도가 되는 식이다.
자, 본격적으로 설명하기에 앞서 오차를 어떻게 극복하는지 좀더 구체적으로 생각해보자. 어려울것 없다. 이전 포스팅에서 다 얘기한 거다.
먼저 드론이 수평상태로 있다고 생각해보자.
검은색이 드론이고, 단순하게 2개의 모터가 있다고 하자. 수평상태, 즉 각도가 0도인 상태를 유지하기 위해서는 두 모터의 추력이 비슷해야한다.
추력이 비슷하단 이야기는 뭘까? 모터의 추력을 조절하는게 뭘까? 바로 모터에 입력되는 전압의 크기이다.
고로, 이 포스팅에서 모터 추력 = 모터에 입력되는 전압크기 라고 보면 된다.
모터의 추력이 강하다 = 모터에 입력되는 전압이 크다.
모터의 추력이 약하다 = 모터에 입력되는 전압이 작다.
이렇게 생각하면 된다.
위와 같은 상태라면, 모터에 들어가는 전압의 크기가 거의 동일할 것이다.
그런데 만약 내가 이상태에서, 드론보고 10도 기울이라고 명령을 줬다고 해보자. 대체 무슨 수로 10도를 기울일 것인가?
모멘트의 개념이 나오는데, 어려울 것 없다. 그냥 1번 추력을 낮추고 2번 추력을 높이면 된다. 그러면 1번은 가라앉고, 2번은 떠서 결과적으로 회전하게 되는 것이다. 즉, 1번 모터에 들어가는 전압을 낮추고, 2번 모터에 들어가는 전압을 높이면 된다. (전압의 크기는 아두이노에서 pwm 신호로 가능하다. 관련 내용은 추후에 포스팅..)
물론, 모터에 들어가는 전압을 너무 낮춰버리면 모터가 돌지 않게되므로 어느정도 선에서 낮춰야한다. 적어도 드론이 떠있을 추력은 가져야할게 아닌가? 예를들어 가만히 있을 때 드론에 인가되는 전압이 10V였다면, 위와 같은 상태에서는 8V 정도 주면 되는 식이다.
자, 이 상태에서 다시 내가 0도로 가라는 명령을 줬다고 하자. 즉, 다시 수평상태를 맞추라는 것이다.
위와 반대과정으로, 1번 출력은 높이고 2번 출력은 낮춰서 다시 반대로 회전시킬 것이다. 그런데 어떻게 정확히 0도를 맞출까? 그냥 회전하다가 얼추 수평맞으면 바로 모터 출력을 갖게 놓으면 될까? 아니다. 드론몸체가 회전하면서 생기는 회전관성이 있기 때문에 그렇게 단순하게는 절대 수평을 잡을 수가 없다.
그렇다면? 아두이노에서 mpu6050을 통해 얻은 각도를 가지고 연산을 해야한다. 즉, 현재 기울어진 각도값과, 목표값인 0도를 계속 비교하는 것이다.
10도 기울어진 상태에서였으므로, 현재값은 10도가 될 것이다.
그러다 모터에 인가되는 전압을 조절하면, 즉 모터 추력을 조절하면 현재값이 9도, 8도, 7도, 하면서 점점 작아진다. 커지다가 3도, 1도, 0도까지 올 것이다. 그런데 0도에 왔으면 더이상 회전하면 안되고 유지해야한다. 어떻게??
바로 오차를 이용하는 것이다. 예시에서 보듯, 10도에서 0도로 기울어질수록 오차가 점점 작아진다. 처음엔 10이었다가 나중엔 0이 되는 것이다.
따라서 오차값을, 1번과 2번 모터에 인가되는 전압의 차이와 연관시키는 것이다.
오차가 10일때는 그만큼 전압차이가 커서 회전하려고 하고, 오차가 0으로 다가갈수록 전압차이가 작아져서 결국 두 모터에는 같은 전압이 인가되는 것이다.
설명이 복잡하군......... 블록다이어그램은 아래와 같다.
제어 공부를 좀 해보면 별로 어렵지 않은 그림인데..
Desired state이 우리가 추구하는 0도이다. 그리고 그 아래 measured state이 바로 현재각도값!
보면 첫번째 동그라미에서 Desired State - measured state이 되게 되어있다. 즉 이게 바로 오차고, 오차가 e(t)라고 표현되어있는 것이다.
그 옆에 네모 3개가 차례대로 P, I, D 제어하는 블록을 나타낸다. 특히 Kp, Ki, Kd를 게인(Gain) 값이라고 한다.
별로 어려운 개념은 아니고, 쉽게 얘기해서 P, I, D 제어의 중요도를 나타내는 지표라고 보면 된다.
이를테면 Kp가 커질수록 PID제어를 하는데 있어서 P 부분의 영향이 더 커지는 셈. 아무튼 하나씩 살펴보자.
먼저 P제어. 비례제어부분이다.
아까 위에서 얘기했듯이, 오차가 크면 그것에 비례해서 전압의 차이가 결정된다. 오차가 0이 되면 전압의 차이도 0이 된다.
그런데, 잘 생각해보자.
기울어진 드론이 0도로 다가왔다고 치자. 이제 오차가 1도밖에 안난다. 그리고 비례제어이기 때문에 처음 전압의 차이보다 10분의 1배가 된 전압 차이가 모터에 인가되고 있을 것이다. 그런데 만약 그 전압차이가 드론을 회전시키기에 충분한 회전력을 발생시킬 수 없다면?
다시말해, 1번과 2번 모터에 분명한 추력차이가 있다. 그런데 그 차이가 너무 작아서 드론을 회전시킬수가 없는것이다. 그렇게 되면 아직 오차가 1도라고 남아있는데, P제어만으로는 영원히~~~~~~ 오차를 0으로 만들 수가 없다는 결론이 나온다. 왜? 힘이 부족하니까 말이다.
다음으로는 I 제어. 적분제어 부분이다.
위에서 P제어만으로는 오차를 0으로 만들 수 없을 수도 있다고 이야기했다. 그래서 I제어를 사용한다. P, I, D 제어는 각각 독립적으로 작용한다!
오차가 10도에서 1도로 줄어들면, P제어는 독립적으로 행동하여, 위와 마찬가지로 처음의 10분의 1배인 전압의 차이를 인가하려고 한다.
그리고 I게인은, 10도에서부터 1도까지 줄어들면서 생긴 오차를 계속 누적한다. 어떻게? 현재 오차와 시간을 곱해줌으로써. 고등학교 수학에서 구분구적법을 생각하면 정확하다. 계속 오차 값을 과거부터 누적해오는 것이 I제어인 것이다.
P제어와 I제어를 같이 하게 되면, 말했듯이 서로 독립적으로 작용한다. 그리고 각각 독립적으로 구한 전압의 차이를 더한 값을, 모터에 인가하게 된다. 따라서 PI 제어를 할 때는 두 제어로 구한 전압 차이를 더한 값을 모터에 인가하게 되는 것이다.
오차가 1도로 줄어들었을 때, P제어는 큰 힘을 발휘하지 못하지만 I제어는 계속 누적해왔기 때문에, 오차가 있는 한 계속해서 전압 차이를 더 늘리게 된다. 현재 오차와 시간을 곱한 것이 I 게인으로 구한 제어값이기 때문이다! 고로 오차가 0이 될때까지 계속 전압의 차이를 만들어내는 것이 I 게인이다.
다음은 D 제어. 미분 제어이다.
이것은 현재의 오차값과, 이전 오차값의 차이를 시간으로 나눈 값이다. 즉, 과거의 오차 값을 전압 차이를 결정하는데 할당시켜 보다 부드럽게 움직이도록 하는 것이다. 정확한 개념은 잘 모르지만, D 제어가 생기게 되면 반응성이 더 부드럽게 나타나게 된다.
아래 움짤을 보면 이해가 편할 것이다.
https://ko.wikipedia.org/wiki/PID_%EC%A0%9C%EC%96%B4%EA%B8%B0
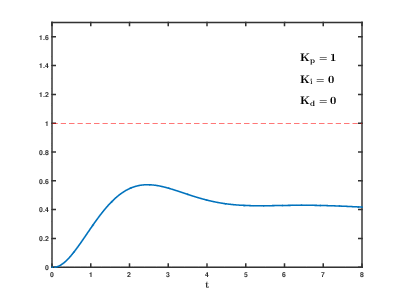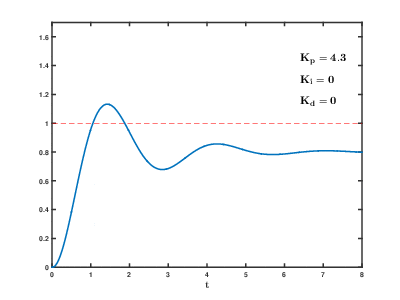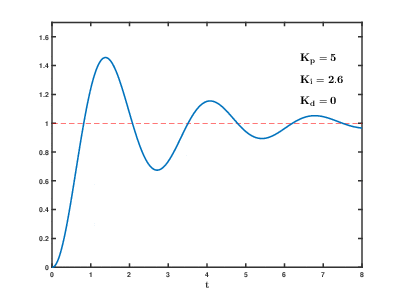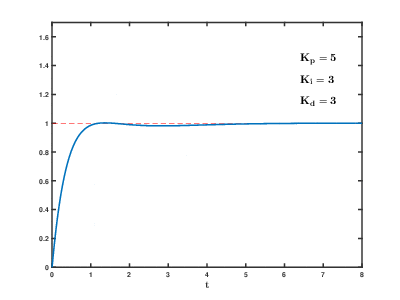
주목해야 할것은, 빨간선이 목표값이란 것이다. 즉 우리로 치면 0도이다.
그리고 파란선이 (0, 0) 지점부터 출발하는데 x축은 시간이고 y축은 현재 각도값이라고 보면 된다. 빨간선이 목표값인 0도이고, y값이 0인데 우리가 생각하는 10도라고 보면 된다.
1. P게인이 점점 늘어난다. 시간이 지날수록 목표값이 더 근접해가는 것을 알 수 있지만, 목표값인 빨간선에 이르진 못하는 것을 볼 수 있다. 아까 얘기했듯이, 오차가 너무 작아서 충분한 전압차이를 인가할 수 없는 것이다.
2. 이 때 I게인을 점점 늘린다. 빨간선에 이르지 못했던 현재 각도값이 쉽게 이르는 것을 알 수 있다. 그런데 동시에 반응이 조금 거칠어 진다. 시간이 지남에 따라 드론이 요동치듯이 목표값에 이르른다. 요동치는 진폭을 보고 Overshoot이라고 한다. 오버슛이 크다는 것은 크게 요동친다는 것. 별로 좋지 않은 제어가 될 것이다.
3. 이 때 D게인을 점점 늘리면, 요동치던 드론이 보다 부드럽게 목표값에 도달하는 것을 볼 수 있다.
사실 쉽게 설명한다고 했지만... 이해가 쉬울지는 모르겠다.
이게 PID 제어의 전부이다.
PID제어는 제어 이론 중에서도 아주 직관적이고 쉬운 제어기법이라고 한다. 굉장히 직관이고, 드론이라는 것의 역학적 모델링을 세우지 않아도 그냥 직관적으로 PID 게인값들을 찾을 수 있다. 어떻게? 실험하면서. 고로!!! 쫄 필요 없다. 이건 굉장히 쉬운 기법이다.
자, 그렇다면 아두이노에서는 어떻게 코딩을 할 것인가?
이건 다음 포스팅에서..
'Developer > Drone DIY' 카테고리의 다른 글
| 드론 DIY | 필수 부품들 구매하기 (0) | 2016.12.21 |
|---|---|
| 드론 DIY | 아두이노 PID 제어 코드 (코드 첨부) (113) | 2016.02.12 |
| 드론 DIY | 드론 PID 제어 이론 1 (3) | 2016.02.11 |
| 드론 DIY | 아두이노 mpu6050 각도 코드 및 이론 (15) | 2016.02.09 |
| 드론 DIY | 아두이노 프로그래밍 (12) | 2015.12.09 |





댓글